Challenge description

Votre ami féru de "homebrews" vous a fourni ce qu'il qualifie de "jeu de combat génial en réseau !" pour votre console "moddée", non sans un petit sourire en coin. Et vous êtes en effet assez dubitatif : son jeu ne semble pas faire grand chose ...
Connaissant les facéties de votre ami, et armé de votre curiosité, vous vous lancez dans l'analyse de ce qu'il vous a fourni en espérant lui prouver que vous relevez le challenge !
The attached binary file is a weird elf file named perfect-cell.self.
Recon
Running file on the binary does not tell us much
$ file perfect-cell.self
perfect-cell.self: data
However by viewing it in a hex viewer we notice a ELF header.
00000000 53 43 45 00 00 00 00 02 00 01 00 01 00 00 03 f0 |SCE.............|
00000010 00 00 00 00 00 00 0a 80 00 00 00 00 00 37 53 e8 |.............7S.|
00000020 00 00 00 00 00 00 00 03 00 00 00 00 00 00 00 70 |...............p|
00000030 00 00 00 00 00 00 00 90 00 00 00 00 00 00 00 d0 |................|
00000040 00 00 00 00 00 17 53 d0 00 00 00 00 00 00 02 90 |......S.........|
00000050 00 00 00 00 00 00 03 90 00 00 00 00 00 00 03 a0 |................|
00000060 00 00 00 00 00 00 00 70 00 00 00 00 00 00 00 00 |.......p........|
00000070 10 10 00 00 01 00 00 03 01 00 00 02 00 00 00 04 |................|
00000080 00 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
00000090 7f 45 4c 46 02 02 01 66 00 00 00 00 00 00 00 00 |.ELF...f........|
And by running file again we see it is a powerpc executable.
$ file file.elf
ELF 64-bit MSB executable, 64-bit PowerPC or cisco 7500, Unspecified or Power ELF V1 ABI, version 1, statically linked, stripped
Having done some reverse-engineering on the PSP, I knew that SCE was
something sony related (present in the syscall names) and that .self
are encrypted/compressed executables for sony consoles. The only PowerPC
based sony console is the PS3.
To be able to play around with the program, I used the rpcs3 emulator
(which can be found here). When launching
the binary, we are met with the following screen:

And not much happens beyond that. As it speaks about a “network shell” we
can run netstat and check whether any port is open:
$ netstat -lpn
Active Internet connections (only servers)
Proto Recv-Q Send-Q Local Address Foreign Address State PID/Program name
tcp 0 0 0.0.0.0:1337 0.0.0.0:* LISTEN 12024/./bin/rpcs3
tcp 0 0 127.0.0.1:2345 0.0.0.0:* LISTEN 12024/./bin/rpcs3
[...]
Lo and behold, a very sus port 1337 is open. By connecting to it with
netcat we are greeted by the following message:
$ nc localhost 1337
____ ____ __ ______ ____
/ __ \___ _____/ __/__ _____/ /_ / ____/__ / / /
/ /_/ / _ \/ ___/ /_/ _ \/ ___/ __/ / / / _ \/ / /
/ ____/ __/ / / __/ __/ /__/ /_ / /___/ __/ / /
/_/ \___/_/ /_/ \___/\___/\__/ \____/\___/_/_/
========================================================
Welcome to Pefect Cell!
Please provide a correct input ...
This is where we will enter our flag !
Reverse-Engineering the ELF
More than simply providing emulation, rpcs3 also provides some nifty
developer oriented utilities, such as dumping the unencrypted ELF
file on disk (Utilities > Decrypt PS3 Binaries).
Loading the ELF as is in a disassembler would work. But to be as comfortable
as possible I used the Ps3GhidraScripts
which provides Ghidra scripts to resolve PS3 syscalls.
I first started to look at the cross-references to the accept function.

Which lands in a wrapper function, that I renamed calls_accept:

This function is called in only one place, which looks like the main
client accept loop for the server:
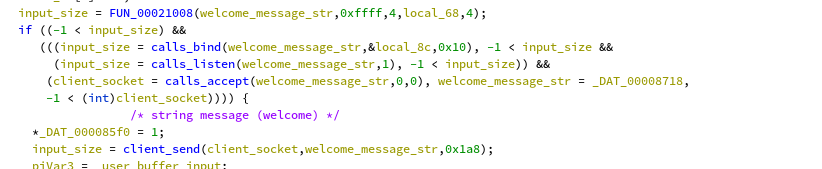
The rest of the function gives us some insight as to the form or our
input. For example the loop only exits if, (1) the input size is
0x67, (2) the first 5 bytes match the value ‘FCSC{‘, (3) the last char
of the input (not counting the ‘\n’) is ‘}’.

If everything matches, this function returns and we land in the function
at address 0x11350. The program continues by setting up some stuff
called SPUs, spu threads, groups, writing to snr (???), and then there
is a memcmp of size 0x60 (which is the size of our input minus the size
of ‘FCSC{}’) and two pointers.

We can already guess that one of them is
our input, and the other our target. To check the assumption, I configured
the emulator to fully interpret the CPU (instead of using a JIT), and
I added the following code to rpcs3/rpcs3/Emu/Cell/PPUThread.cpp:
void ppu_thread::exec_task()
{
// ...
if (u64{cia} == 0x11628)
{
uint8_t user_input[0x60] = {};
uint8_t cst_check[0x60] = {};
std::printf("user input ptr: 0x%lx cst_check_ptr: 0x%lx\n", gpr[30], gpr[4]);
std::memcpy(user_input, vm::base(gpr[30]), 0x60);
std::memcpy(cst_check, vm::base(gpr[4]), 0x60);
std::printf("user_input: 0x%lx\n", gpr[30]);
for (unsigned i = 0; i < 0x60; i++)
{
std::printf("%02x ", user_input[i]);
}
std::printf("\n");
std::printf("cst_check: 0x%lx\n", gpr[4]);
for (unsigned i = 0; i < 0x60; i++)
{
std::printf("%02x ", cst_check[i]);
}
std::printf("\n");
}
If we input a flag with all ‘A’s we get the following output:
user input ptr: 0x30000100 cst_check_ptr: 0x10001fd8
user_input: 0x30000100
a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 a4 f3 c0 e2 4d db 77 4d 1e f3 c0 e2 4d db 77 4d 1e cf 19 f5 d2 ed f7 71 0c cf 19 f5 d2 ed f7 71 0c af af af af af af af af af af af af af af af af 49 3b ac 1e 49 3b ac 1e 49 3b ac 1e 49 3b ac 1e 5e c8 5e c8 5e c8 5e c8 5e c8 5e c8 5e c8 5e c8
cst_check: 0x10001fd8
05 d2 5a cb 9f 61 24 2e 24 90 c3 0e c3 dc 1b a6 92 dc 21 66 bb a1 3c 99 92 0a 21 75 24 9d 5d 6a c9 b2 58 0f 30 87 5b 47 46 07 fa 45 38 4d e8 4c ab 9d be 5b a7 cd a7 7b 1f 04 fe 86 78 5d cb 49 1b 8b d3 82 5a 7e cb a7 2a 2a 52 bc 73 77 b9 79 78 3a ae c4 6b 19 e8 a5 a7 75 fb 46 05 d3 82 b5
We can already notice that our input was modified in a seemlingly linearish
fashion for parts of it. And apart from a few places, it seems to have been
modified in 16 bytes chunks (6 chunks of 16). Now we only need to reverse
the algorithm used for the transformation… wait, what was that SPU thing
again ??
Cell architecture and the SPU(s)
The PS3’s CPU is called Cell and it is known for being exotic and complex.
It is architectured in the following way:
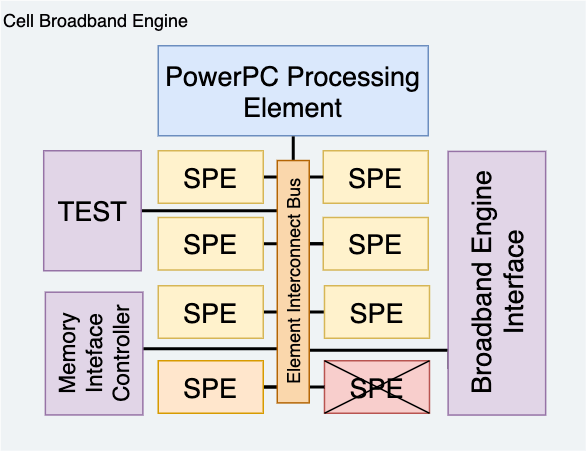
First there is the main unit, the PowerPC Processing Element (or PPU).
The code we analyzed so far concerns this elements. Then there are 7 powerful
coprocessors called Synergistic Processor Unit (or SPU), which run on
a different architecture and are orchestrated by the PPU. They act as
accelerators and custom code can be uploaded to them. A very good resource for
understanding more about them is the very good blogpost made by Rodrigo Copetti
(https://www.copetti.org/writings/consoles/playstation-3/).
Now let’s take a look back at the code between our read and the memcpy check:

In (1) 6 SPUs are initialized, then in (2) an image (spu code) is loaded,
then finally the SPU threads are configured with their index and our input.
As our input is 96 bytes long, and as 6 SPU’s are spawned, we can guess that each
of them will separately process 16 byte chunks of input.
By again injecting code in the PPU interpreter, the SPU image can be recovered
during the call to sys_spu_image_import.
$ file spu_bin.elf
spu_bin.elf: ELF 32-bit MSB executable, Cell SPU, version 1 (SYSV), statically linked, stripped
Reversing the SPUs code
Even though the SPU architecture is exotic, some reverse-engineering tools have
been extended to support it. For reverse-engineering the code I used the
GhidraSPU project to be able to analyze
it in ghidra.
Before delving into the analysis of the code, I wanted to understand what kind of
architecture I was up against. A particular sentence in the architecture manual
sent chills down my spine:
The SPU architecture defines a set of 128 general-purpose registers (GPRs), each of which contains 128
data bits. Registers are used to hold fixed-point and floating-point data. Instructions operate on the full width
of the register, treating the register as multiple operands of the same format.

Reverse-Engineering SIMD heavy code (at least for me) is extremely painful as
the data can be broken up into chunks of different sizes, which can be interpreted
differently from an instruction to the next. To add insult to injury this architecture
has 128 SIMD REGISTERS. But anyway, a flag is a flag and now we are in too deep to go
back.
Descent into madness
Now begs the question of the strategy to take to solve this challenge. As seen
previously, on at least parts of the input, the transformations seem at first
glance simple enough and could be simple substitutions. If this is the case
a bruteforcing approach could be envisioned where we would bruteforce one by one
the bytes of the input. However this would require repurposing the code of the
emulator to extract only the SPU emulation code, which would incur significant
engineering work. However by doing this we could completely forget about the
abomination that is the SPU and treat it as a blackbox.
The other approach would be the classical one of fully reverse engineering the
SPU code and try to inverse the algorithms transforming our flag (or bruteforcing
the algorithm if needed). This requires looking at the code, and from a cursory
glance this is a big no no. But in the end, I selected this method.

I spent about 15h hours reading the machine code line by line and reimplemented
every relevant instruction in python. I do not recommend.
Methodology
As seen previously, 6 SPUs are launched to transform our input. To be able to
follow the transformation of the input data and the operations, I chose to
debug the code through execution traces. This can be done by setting the SPU
emulation mode to interpreter and by injecting the following code in
rpcs3/rpcs3/Emu/Cell/SPURecompiler.cpp:
std::ofstream* streams[8] = {};
void trace_open()
{
if (!streams[0])
{
for (unsigned i = 0; i < 8; i++)
streams[i] = new std::ofstream(fmt::format("spu_%u.trace", i));
}
}
void spu_recompiler_base::old_interpreter(spu_thread& spu, void* ls, u8* /*rip*/)
{
// ...
trace_open();
*streams[spu.index] << fmt::format("--- pc: 0x%08x ---\n", spu.pc);
std::string regs;
for (unsigned i = 0; i < 128; i++)
{
*streams[spu.index] << fmt::format("r%u=", i);
uint8_t* number = reinterpret_cast<uint8_t*>(&spu.gpr[i]);
for (unsigned j = 0; j < 16; j++)
*streams[spu.index] << fmt::format("%02x", number[15-j]);
*streams[spu.index] << '\n';
}
streams[spu.index]->flush();
This gives a trace of the program counter as well as all gprs, which is enough
for our purpose. Using execution traces is great for reverse engineering as it
allows to record the full execution of a program, then go back and forth to
any point in the execution which greatly speeds up the process of following the
data and understanding the behavior of instructions.
The function treating the first chunk starts at 0x5d0 and is one of the
simple ones.

In (1), the input is modified by substracting a value from it.
In (2), the bytes of the input are rotated using the rotqby instruction.
This instruction operates on the level of bytes (rotqby of 2 means rotating by
16 bits). Afterwards a shuffling mask is computed using cbx and it is applied
with the shufb instruction. As these rotations and shuffles don’t depend on
the input, using the execution trace we can simply get the value before and
after the loop to extract the shuffling constants.
In (3) there is this time a rotation at the bit level with the instruction
rotqbii.
In (4) things get interesting. The shuffled and rotated bytes of the input
are used as an index in a 256 bytes buffer of constants. This is done in the
following way:
1: ai off, base, input_char
2: lxq cst, base, input_char
3: ai off, off, 0xd
4: rotqby s, cst, off
5: shufb result, s, ..., ...
In 1 the extracted input character value is added to the address of the array
into an accumulator. In 2 the lxq instruction is used to load a 16 bytes
constant from the array, do note that the offset base+input_char is aligned
to 16 bytes before the load. In 3, 12 is added to the original offset. Rotqby
is used with this offset to do a byte rotation on the constant array. Finally
in 5 the shuffle instruction is used to extract a byte from the rotated constant
to be placed in the resulting output (depending on the mask the shufb
instruction can be used for shuffling or specific byte extraction).
From there it is not apparently clear how this is reversible, but by looking
at the constant array itself we can devise a plan:
0x32, 0xa5, 0x2b, 0xdf, 0xac, 0xd9, 0xcd, 0xc1, 0xef, 0x3a,
0x84, 0x2c, 0x53, 0x3c, 0xff, 0x9a, 0xeb, 0x16, 0xd3, 0x3f,
0xbc, 0xc4, 0x31, 0x47, 0x12, 0x96, 0x75, 0x90, 0x8a, 0xc5,
0xbf, 0x43, 0x7a, 0x64, 0xb5, 0xc6, 0xaa, 0xa1, 0x22, 0x48,
0xf9, 0x99, 0x08, 0x34, 0x65, 0xa3, 0x98, 0x44, 0xa0, 0xe0,
0x6b, 0xb6, 0xbe, 0xce, 0xfc, 0x03, 0xa6, 0xa4, 0x35, 0x5e,
0x11, 0xd7, 0x76, 0x05, 0x0e, 0xf4, 0xa2, 0xae, 0x70, 0x6f,
0x78, 0x9c, 0x09, 0x4c, 0x17, 0xf0, 0xd8, 0x56, 0xfd, 0x15,
0x71, 0xf3, 0xfb, 0x1d, 0xb7, 0xa7, 0x66, 0x9f, 0xb3, 0x79,
0xc3, 0xb4, 0x5d, 0x5b, 0xab, 0xd6, 0x94, 0x1e, 0xc0, 0x0c,
0x9d, 0x04, 0x7f, 0xe4, 0x6a, 0x4b, 0x9b, 0xe8, 0x0d, 0x86,
0x82, 0xea, 0x52, 0xdb, 0x51, 0xd4, 0xb0, 0xb9, 0xa8, 0x61,
0x6d, 0xe6, 0x97, 0x7c, 0xad, 0xcb, 0xda, 0x88, 0x68, 0x1c,
0x07, 0x00, 0x30, 0x6c, 0x50, 0x59, 0x3e, 0x40, 0x20, 0xde,
0xf1, 0xf5, 0x0f, 0xa9, 0x5c, 0x4d, 0x89, 0x21, 0xbd, 0xe2,
0x57, 0x0b, 0x67, 0xc7, 0x87, 0xc2, 0xd2, 0xdc, 0x18, 0x93,
0x8e, 0x36, 0x77, 0x8c, 0xe5, 0x4e, 0x9e, 0x39, 0x60, 0x80,
0x73, 0xfa, 0xfe, 0x0a, 0x81, 0xed, 0xb1, 0x2f, 0xf6, 0xba,
0x58, 0xee, 0x85, 0x45, 0x38, 0xd5, 0x4a, 0xe7, 0x5f, 0x2e,
0xf7, 0x91, 0x2d, 0x95, 0x7d, 0xb8, 0x7e, 0x1f, 0x49, 0x02,
0x63, 0xe3, 0x2a, 0xe1, 0x10, 0xca, 0x06, 0x27, 0x37, 0x69,
0x3b, 0x83, 0x8f, 0x92, 0x13, 0x55, 0xcc, 0x29, 0x54, 0x26,
0x14, 0x1a, 0x1b, 0x41, 0xd1, 0x42, 0x46, 0xec, 0x62, 0x74,
0xd0, 0x28, 0x3d, 0x8b, 0xf8, 0xcf, 0x7b, 0xb2, 0x4f, 0x6e,
0xc8, 0xdd, 0x33, 0x23, 0xf2, 0xaf, 0x72, 0x24, 0xe9, 0x01,
0x19, 0x8d, 0xbb, 0x25, 0xc9, 0x5a
This 256 bytes array contain only unique values from 0 to 255. Which means
that for any output byte, we can find the original with some tricks !
By taking the output byte we can find back the correct 16 byte value in
which it appears, which gives us the offset from the start of the array,
minus the alignment. By then computing the shift in position of our
byte compared to the same in the original array, we get the missing nibble
in the offset ! By substracting the offset we computed from the base address
of the array, we get the original input value.
Finally in (5), the input is written back to the main processor.
The algorithm can be reversed with the following piece of code:
def input_0_rev(value):
input_0_unshuffle = [5, 9, 8, 4, 1, 0, 10, 12, 11, 15, 14, 7, 13, 2, 3, 6]
result = [0]*16
r15 = [0]*16
# Invert last loop
for i in range(16):
r22_3 = value[16 - i - 1]
r19_off = 0
for j in range(0, len(constant_table_1730), 16):
cst = constant_table_1730[j:j+16]
if r22_3 in cst:
# j is the offset from the base of the array, aligned on 16 bytes
r19 = cst.copy()
r19_off = j
break
else:
# Should not happen
raise Exception("")
# Add the shift to the offset which gives us the original value
r19_off += r19.index(r22_3)
r15[16 - i - 1] = r19_off
r12 = r15
inv_r2 = ilh(0xeeef) # Add the inverse of the constant
r5 = ah(r12, inv_r2)
r5 = inv_rotqbii(r5, 5) # Inverse the bit shift
result = [0]*16
# Unshuffle (first loop)
for i, e in enumerate(input_0_unshuffle):
result[i] = r5[e]
return result
Running this with the first 16 bytes of the expected bytes (the constant array
in the memcmp), we get the string 30gbt9RzIif5L_s7.
This is the part of the challenge that tooks the most time to solve. The checking
function starts of very innocently with only a few instructions (at 0x6ac):
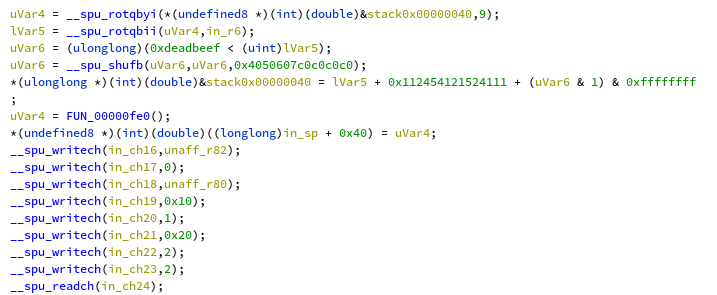
This does a few computations and then calls the sub_fe0 function with the
transformed input as an argument. The called function is simply massive to
unpack:

It does not look scary in the decompiler, however it is only composed of a series
of shifts, loads, rotations, using at least 20 different registers moving data
around. I spent about a full day on this function reimplementing it in python
all the while comparing with the execution traces checking for correctness. In the end
the algorithm is similar to the first function, except that it processes 8 bytes
of input at a time:
def sub_fe0_rev(r3):
def bruteforce_char(rev_reg):
# Find the only non null input in reg
for i in range(len(rev_reg)):
if rev_reg[i] != 0:
idx = i
break
else:
raise Exception("noop")
# Bruteforce char
for j in range(256):
constant = lxq_1730_i(j)
shift = (0x1730 + j + 0xd) & 0xf
res = rotqby(constant, shift)
if res[idx] == rev_reg[idx]:
return j
raise Exception("nop")
res = []
for i in range(2):
chunk = [0]*8
value = r3[i*8:(i*8)+8]
# input_0
r63 = [0]*16
r63[0] = value[0]
r62 = shrb(r63, 0xf)
r46 = rotqby(r62, 0x8)
r42 = shlb(r46, 0x4)
chunk[0] = bruteforce_char(r42)
# input_1
r74 = [0]*16
r74[6] = value[6]
r73 = shrb(r74, 0x9)
r59 = rotqby(r73, 0x8)
r54 = shlb(r59, 0x4)
chunk[6] = bruteforce_char(r54)
# input_2
r4 = [0]*16
r4[5] = value[5]
r5 = shrb(r4, 0xa)
r64 = rotqby(r5, 0x8)
r60 = shlb(r64, 0x4)
chunk[5] = bruteforce_char(r60)
# input_3
r16 = [0]*16
r16[4] = value[4]
r2 = shrb(r16, 0xb)
r72 = rotqby(r2, 0x8)
r68 = shlb(r72, 0x4)
chunk[4] = bruteforce_char(r68)
# input_4
r55 = [0]*16
r55[7] = value[7]
r51 = shlb(r55, 0x4)
chunk[7] = bruteforce_char(r51)
# input_5
r20 = [0]*16
r20[3] = value[3]
r14 = shrb(r20, 0xc)
r78 = rotqby(r14, 0x8)
r75 = shlb(r78, 0x4)
chunk[3] = bruteforce_char(r75)
# input_6
r18 = [0]*16
r18[2] = value[2]
r24 = shrb(r18, 0xd)
r10 = rotqby(r24, 0x8)
r8 = shlb(r10, 0x4)
chunk[2] = bruteforce_char(r8)
# input_7
r12 = [0]*16
r12[1] = value[1]
r26 = shrb(r12, 0xe)
r11 = rotqby(r26, 0x8)
r7 = shlb(r11, 0x4)
chunk[1] = bruteforce_char(r7)
res += chunk
return res
The top function can then be inverted as well with the following code:
def input_1_rev(value):
rev_value = sub_fe0_rev(value)
r60 = u128_to_reg(0xfeedbabedeadbeeffeedbabedeadbeef)
r65 = u128_to_reg(0x04050607c0c0c0c00c0d0e0fc0c0c0c0)
r63 = u128_to_reg(0x00000000ffffffff00000000ffffffff)
m = inv_sfx(r63, r60, rev_value)
m = inv_rotqbii(m, 6)
m = rotqby(m, 7)
return m
By passing the second 16 bytes slice of the constant to this function we get the
string 0cRm7gXHm_R-8WkK.
After ~7h spent suffering on the previous function alone, the third one was a
godsend (at 0x6e8).
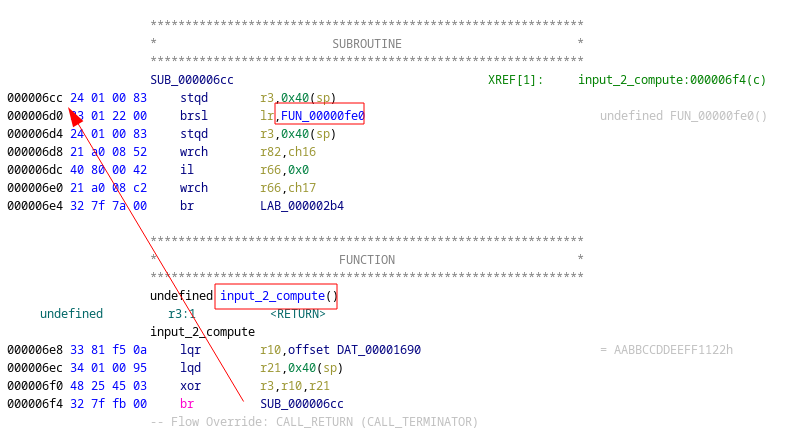
It simply xors the passed input with a constant, calls the previously reversed
horrible function, and forwards the result to the main processor. As such only
the xor needs to be reversed:
def input_2_rev(value):
rev_value = sub_fe0_rev(value)
cst = u128_to_reg(0xaabbccddeeff1122aabbccddeeff1122)
return xor(rev_value, cst)
Passing the third 16 bytes slice of the constant array gives the string
TVxSjeL5H9gjVnzk.
This function at 0x6f8 follows the models of the previous ones, only again
differing in the number of bytes processed at a time.

In (1) we have the usual shuffle. In (2) some bit and byte level rotations
as well as a not. In (3) the transformation of input bytes in a loop executing
6 times. And finally in (4) we have the same thing. I don’t know if it is a compiler
shenanigan or voluntary, but the work done outside the last loop looks identical to the one
done inside.
After reimplementing the parts (1) to (3) of the function, I tried to add
two iterations two my second loop (from 6 to 8), and after comparing with execution traces
I could confirm that this simplification was correct. The following python code can reverse
the fourth step:
def input_3_rev(value):
def bruteforce_char(rev_reg):
# ...
rev_input = [0]*16
for i in range(8):
r16 = [0]*16
r19 = [0]*16
r16[2] = value[i*2]
r19[3] = value[(i*2)+1]
r14 = shrhi(r16, 0x8)
rev_input[i*2] = bruteforce_char(r14)
rev_input[(i*2)+1] = bruteforce_char(r19)
rev_input = nor(rev_input)
rev_input = inv_rotqbii(rev_input, 3)
rev_input = rotqby(rev_input, 16-5)
# Now unshuffle
shuffle = [14, 15, 12, 13, 6, 7, 2, 3, 0, 1, 4, 5, 8, 9, 10, 11]
result = [0]*16
for i, e in enumerate(shuffle):
result[i] = rev_input[shuffle[i]]
return result
Passing it the fourth slice of our constant array gives the string SJBg3y4prWG4tU_5.

The fifth function at 0x250 starts of with simple xors and shuffles. The shuffled
input is then passed to a function and the result is sent to the main program.
Remembering the dreaded function at 0xfe0 I did not feel so good at first, but
in the end it does not look so bad:

The loop in (2) is executed twice and processes 4 bytes of input. As the parts
(1) and (3) are pretty similar to the loop body, we can make the assumption
that this is the same outlining issue as the previous function. After reimplementing
in python, I confirmed that again, simplifying the code again by adding two iterations
to the loop body gave the exact same result. The code to reverse this step is the following:
def sub_dd0_rev(value):
def bruteforce_char(rev_reg):
# ...
res = []
for i in range(0, 16, 4):
r20 = lxq_1730_i(value[i])
r24 = lxq_1730_i(value[i+2])
r17 = lxq_1730_i(value[i+3])
r22 = lxq_1730_i(value[i+1])
r0 = [0]*16
r1 = [0]*16
r2 = [0]*16
r3 = [0]*16
r0[3] = value[i]
r1[3] = value[i+1]
r2[3] = value[i+2]
r3[3] = value[i+3]
chunk = [
bruteforce_char(r0),
bruteforce_char(r1),
bruteforce_char(r2),
bruteforce_char(r3),
]
res += chunk
return res
def input_4_rev(value):
rev_input = sub_dd0_rev(value)
# unsuffle
shuffle = [12, 13, 14, 15, 4, 5, 6, 7, 0, 1, 2, 3, 8, 9, 10, 11]
res = [0]*16
for i in range(16):
res[i] = rev_input[shuffle[i]]
return xor(res, u128_to_reg(0x87934520879345208793452087934520))
Passing the fifth slice to this function gives the string -10yxW8uYzWNMY54.
Fun fact, it is at this step that my monkey brain finally clicked and saw
the similarities between the different transformation functions (shuffling +
byte translation + misc operations for obfuscation). It clicked after about
20h into the challenge. Noticing this early would have saved a LOT of time,
and it was a harsh reminder that sometimes your really need to step back and
see the bigger picture.
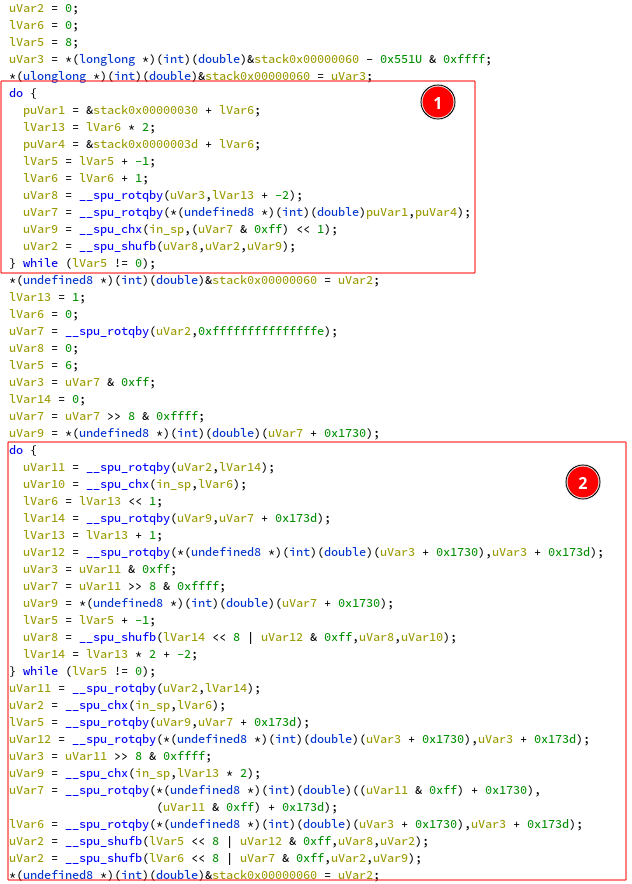
The structure of this function (at 0x420) is eerily similar to the fourth one.
At this point I was too lazy to reverse it properly. I just copy-pasted the
solving code for the fourth step and fiddled with it until it worked.
def input_5_rev(value):
def bruteforce_char(rev_reg):
# ...
rev_input = [0]*16
for i in range(8):
r16 = [0]*16
r19 = [0]*16
r16[2] = value[i*2]
r19[3] = value[(i*2)+1]
r14 = shrhi(r16, 0x8)
rev_input[i*2] = bruteforce_char(r14)
rev_input[(i*2)+1] = bruteforce_char(r19)
rev_input = rotqby(rev_input, 0)
# Now unshuffle
shuffle = [14, 15, 12, 13, 6, 7, 2, 3, 0, 1, 4, 5, 8, 9, 10, 11]
result = [0]*16
for i, e in enumerate(shuffle):
result[i] = rev_input[shuffle[i]]
return ah(ilh(0x551), result)
Passing the last slice of bytes of expected bytes to this function gives out
the string ssDcpRHfKZ8KZkX3.
Now just concat the strings …

… and send them to the game for confirmation !
$ nc localhost 1337
____ ____ __ ______ ____
/ __ \___ _____/ __/__ _____/ /_ / ____/__ / / /
/ /_/ / _ \/ ___/ /_/ _ \/ ___/ __/ / / / _ \/ / /
/ ____/ __/ / / __/ __/ /__/ /_ / /___/ __/ / /
/_/ \___/_/ /_/ \___/\___/\__/ \____/\___/_/_/
========================================================
Welcome to Pefect Cell!
Please provide a correct input ...
FCSC{30gbt9RzIif5L_s70cRm7gXHm_R-8WkKTVxSjeL5H9gjVnzkSJBg3y4prWG4tU_5-10yxW8uYzWNMY54ssDcpRHfKZ8KZkX3}
Well done, this is a win! :-)
Afterword
Even though it was a really painful experience, the idea behind this challenge
was really cool. It is a clear evolution of last year’s 2ndMix
challenge, and it is always fun to reverse homebrews on weird architectures.